Integral Canonical Models for Automorphic Vector Bundles of Abelian Type

I’ve uploaded my first paper to the arxiv: http://arxiv.org/pdf/1605.02717v1.pdf

I construct a bunch of integral models for well known objects, mainly building on Kisin’s first integral models paper. Firstly I extend his models for Shimura varieties to models defined over rings like (his are over rings more like )

Secondly, and much more substantially, I construct integral models for what Milne calls the “Standard Principal Bundle”, which is a gadget that in particular allows one to construct automorphic vector bundles, but also to have a notion of “de Rham sheaves” and (with a little more work: another paper is on the way) (iso)crystals.

A useful vague way to think about such objects is the following. A Shimura variety is a moduli space of Tannakian subcategories of a certain shape (roughly that they look like Rep G) of a category slightly larger than the category of motives, together with a trivialization of the etale cohomology fibre functors (the “level structure”). The level structure is needed because otherwise one gets some kind of Artin stack it’s difficult to work with. The Standard Principal Bundle parameterizes the same thing but also throws in a trivialisation of the de Rham cohomology fibre functor, making it a G-torsor over the Shimura variety.

Of course, there are technical issues with this description, but it gives you a good idea of how the construction should go: essentially I handle the Hodge type case by systematically exploiting the de Rham cohomology of the universal abelian variety. I handle the case where G is a torus by using the theory of Kisin modules and their relation to lattices in de Rham cohomology (to get a uniqueness statement), and the theory of CM motives (to get existence). I then do some group theoretic gymnastics to pass from the Hodge and torus type cases to the general abelian type case.

Please let me know if you find any mistakes, and I hope you enjoy the paper. 🙂

Cyclotomic Fields and Fermat’s Last Theorem Tutorial Notes and Problems

During Spring Semester 2015 I am teaching an undergraduate course on “Cyclotomic Fields and Fermat’s Last Theorem” at Harvard.

Meeting times and places are currently:

Mondays 4:15-5:45 in SC530

Wednesdays 4:30-6 in SC530.

The latest edition of the notes is here: Cyclotomic Fields and FLT. Please email me any corrections.

The problem sheets are below.

Problem Sheet 1 (due Feb 24)

Problem Sheet 2 (due March 10th)

Problem Sheet 3 (due March 30th)

Problem Sheet 4 (due on Jefferson’s birthday)

Problem Sheet 5 (due April 27th)

Galois descent for transcendental extensions

In this note, I want to discuss the work of Weil as presented in Milne’s papers (in particuar this one). Given a finite Galois extension of fields, many readers will be familiar with the usual “Galois descent” procedure giving an equivalence between (for example) affine varieties over and affine varieties over with a suitable action. Indeed, such extensions are finite etale, and the result is immediate from the general theory of etale descent and the “Galois isomorphism” , which one can unravel and check implies that to give a -action is to give a descent datum.

 

If is no longer finite, this method breaks down. It will still be an fpqc cover, so descent theory works fine, but the Galois isomorphism breaks down. This can be seen using infinite Galois theory: for example by considering and noting that only the open index 2 subgroups give rise to degree 2 etale algebras. In the case where is algebraic and ind-Galois, is profinite and imposing continuity conditions like the one we saw above, one is able to recover Galois descent theory from the finite case. However, if the extension is transcendental, it is less clear how to proceed. For example, a key obviously interesting example is when one has an object over together with an action of . Here has uncountable transcendence degree.

Before we state our theorem, let us first (following Milne) make the question at hand a little more precise. Let be a variety (geometrically reduced separated scheme of finite type) over a field which we assume is algebraically closed (to avoid having to define “Galois”). Let be a subfield. A descent system for is a collection of isomorphisms one for each satisfying the cocycle condition . We emphasise that such a thing is generally not the same as a descent datum. If there is a model giving rise to by base change, we say is effective.

Theorem (Weil): Let be an algebraically closed extension of infinite transcendence degree, and suppose we are given a quasiprojective variety over with descent system to as above. Then for to be effective it suffices for there to be a finitely generated subextension  such that the restriction of to is effective.

Milne notes the following consequence. Suppose your variety over has the following properties.

1. There is a finite set of points such that any automorphism of which fixes each point of must be the identity.
2. There is a finitely generated extension with the property that for all .

Then the given pair is effective for descent .

Indeed since is quasiprojective we may always fix any model for it and enlarge to contain the coefficients of the polynomials describing the variety and the points of . Thus we obtain a model and the condition (2) implies that the isomorphisms coming from the model and the given agree on where they send the points . They therefore agree by condition (1), so we have established effectivity of the restriction of to . The desired result now follows from the theorem.

 

As far as I can see, this seems to give a very practical tool for performing descent along transcendental extensions, and is necessary for Milne to show that Langlands’ conjecture on conjugation of Shimura varieties actually really implies the existence of canonical models.

 

 

Mumford’s Hodge type Shimura varieties (not of PEL type)

In his note A Note of Shimura’s Paper “Discontinuous Groups and Abelian Varieties” Mumford constructs a Hodge type Shimura variety (a family of polarised abelian fourfolds with level structures) that is not of PEL type. He makes the necessary group from a quaternion algebra over a totally real field which is engineered to admit a symplectic representation which is absolutely irreducible (so the resulting abelian varieties cannot admit extra endomorphisms).

More specifically, let be a cubic totally real field. We wish to carefully choose a quaternion algebra such that admits a symplectic representation.

The trick is to note that corestriction on Brauer groups associates to a quaternion algebra , equipped with a natural map . In particular, if we can arrange for to be split, we will certainly get a natural (8-dimensional) representation of . By then imposing some conditions at infinity we can produce a symplectic structure on this representation, realising the resulting Shimura variety as one of Hodge type.

These conditions can be realised: just take to be ramified at any even number of places above each place of , and at two of the three places at infinity.

Then , and unravelling the construction one sees that the map factors where the first map is the standard degree 2 isogeny and the second is given by the natural action on , and visibly preserves the natural symplectic pairing coming from the product of orthogonal and symplectic pairings on these two spaces. Symplectic structures descend, giving the required map

  over .

One extends this game to a Hodge type Shimura datum by taking 

, which is an extension of the image of by landing in .

One takes the Hodge structure to be the composite of with the map taking to on the factor of and the standard 2-dimensional embedding into the factor. It is obvious this extends to give the Siegel Shimura datum on , so we have a Shimura datum of Hodge type, as required.

 

 

 

Differential equations with regular singularities

In this short post I want to note Deligne’s classic result on vector bundles with flat connections (let’s call them “differential equations”: terminology justified by the `cyclic vector theorem”) and give a stupid example illustrating the basic shape of things. I should thank Ananth Shankar for helping unconfuse me faster than I could unconfuse myself.

 

Let be a smooth algebraic variety over . A vector bundle on is a locally free coherent (Zariski) sheaf , and a connection is an additive map of sheaves

 

satisfying the Leibniz law. There is the usual notion of flatness of a connection. A morphism between two such objects is an -linear map between the underlying sheaves making the obvious square commute.

 

One can also make the exactly parallel construction over the complex manifold . Given an algebraic differential equation, we can analytify it and obtain an analytic differential equation:

Deligne’s result gives a functor in the other direction (let’s call it RH for “Riemann-Hilbert”)

.

Theorem (Deligne): The functor RH (exists and) is fully faithful, and the essential image is characterised by taking a good compactification of and restricting to those differential equations with regular singularities at the boundary.

This is a little counterintuitive at first. One imagines there being “more” objects in than in because one can write down more connections, but actually the extra freedom causes more stuff to become isomorphic, resulting in a “smaller” analytic category. Of course, one has but not (unless is proper) an identification in the other direction.

 

Let’s see what happens in a stupid example. Let and the trivial line bundle. Let’s take our favourite non-vanishing algebraic section , and observe that any connection is automatically flat and determined by

(since any other section can be written as which by Leibniz is given by

).

If let us denote by the connection taking .

 

Let’s suppose we have a map between two such differential equations. Let , and the compatibility of with the connections gives the relation

.

In other words, must satisfy a first order differential equation, and in fact we see that up to a constant factor

which is never algebraic unless .

 

The upshot is that in the algebraic category each gives a distinct differential equation, while in the analytic category one can use the above recipe to construct isomorphisms between each of the and in particular they are all equal to , which is the unique algebraic connection with regular singularities at .

 

 

Emerton’s approach to Fontaine-Mazur and density of modular points in big deformation rings

I’m about to give a talk on how to conclude lots of cases of Fontaine-Mazur for 2-dimensional -representations from Emerton’s study of completed cohomology. For this to work, one needs Bockle’s arguments after Gouvea-Mazur and Coleman to deduce “big” R=T theorems from “small” ones which are not too difficult given the success of the original Taylor-Wiles-(Diamond?)-Kisin approach. I attach a set of notes saying roughly how this works and giving references to the literature.

Frobenius and the Hodge Filtration in Crystalline Cohomology

Today I’ve found myself mainly thinking about the interaction between Frobenius and the filtration on crystalline cohomology, referring to Mazur’s classic paper http://projecteuclid.org/download/pdf_1/euclid.bams/1183533965 as well as Ogus’ paper on “Griffiths Transversality in Crystalline Cohomology” and thought I would record a summary here before I forget everything. Of course, both of these papers are from the 1970s, so if there has been any significant advance or later examples of interest that any readers know of I’d be extremely interested to hear.

Firstly the setup. Let 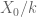be a smooth projective variety over a perfect field of characteristic , and let us also suppose we have a smooth proper lift . We can form the crystalline cohomology and have comparisons 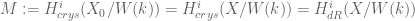. Let us assume these are free modules and in fact also that the Hodge cohomology groups 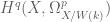are free. Then we have the further relation that .

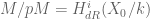What structures are in play? Algebraic de Rham cohomology comes with a Hodge filtration (which depends on the lift , though of course mod it does not), and crystalline cohomology is equipped with a semilinear Frobenius (which does not depend on the lift).

The fundamental relationship between these two structures is given by a theorem of Mazur, which implies under the freeness assumptions we have made that the Frobenius determines the mod Hodge filtration.

Theorem (Mazur): The reduction mod of 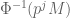is precisely the reduction of .

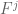(Note for the statement that Frobenius induces an isomorphism 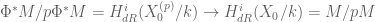preserving the Hodge filtration.)

One immediate consequence of this is the conjecture of Katz relating the slopes of Frobenius to the shape of the Hodge filtration.

Corollary: For the crystalline cohomology of 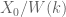, the Newton polygon lies above the Hodge polygon.

We do not explain what this means here, except to remark that Mazur’s theorem allows you to find bases in which the matrix for 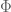has columns divisible by powers of of widths given by the Hodge numbers. The statement, which is about relating these numbers to valuations of eigenvalues, is then just an easy result in linear algebra.

The next obvious question is what can we say about the Hodge filtration 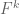coming from our smooth lift? The above result tells us that

.

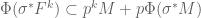Mazur was also able to prove that , where .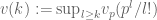

Question (Mazur): Is it in fact the case that 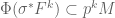? If so, we say is strongly divisible, and this statement is equivalent to Frobenius inducing an isomorphism .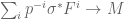

Note that whenever the Hodge filtration has length shorter than , this is immediate from Mazur’s second inequality, since 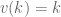in this case for all nonempty pieces of filtration. For example, for the cohomology of a curve or 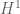of an abelian variety we do get something strongly divisible.

The reason for the distance between Mazur’s estimate and the notion of strong divisibility is the phenomenon of Griffiths transversality, which was investigated by Ogus in the crystalline context following Griffiths’ work in classical Hodge theory.

Classically suppose you have a variety and you want to study its de Rham cohomology. Using the Gauss-Manin connection, one can identify the cohomology group itself with the cohomology of the constant family 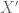defined by the fibre at . However, the Hodge filtrations will not agree, but are allowed to vary within the confines imposed by Griffiths transversality. Explicitly, one can show that

.

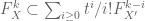In the crystalline situation, given two smooth lifts 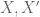, one obtains a similar formula,

.

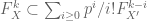However, note that the denominators start to cancel off the powers of , once , and this is exactly why Mazur can only get the estimate involving . For a more general statement in the same vein see Ogus’ “corollary 2.5.”

These are all inequalities, and it is natural to ask if they are “strict”. In other words, does Griffiths transversality really happen (do these filtrations vary), and to what extent? One obvious example to bear in mind is abelian varieties, where every possible lift of the Hodge filtration corresponds to a lift (and determines it uniquely: this is Grothendieck-Messing theory). If, as the filtration lengths increase, there is enough freedom for the lifts to vary widely within the constraints imposed by transversality, then one would expect a counterexample to strong divisibility.

Ogus manages precisely this, and his example is as follows. Suppose 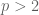, and consider the hypersurface 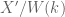given by

.

Then 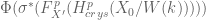fails to lie in .

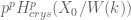This is achieved by comparing to the Fermat hypersurface which also visibly lifts the special fibre. One can show that in fact the cohomology of this is strongly divisible, exploiting the fact the group actions in play give an explicit decomposition of the cohomology, making it easy to control. Comparing the filtration coming from this to the filtration coming from 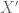, using a careful deformation-theoretic study of these differences, Ogus deduces that the latter fails to be strongly divisible.

 

Seminar on p-adic Langlands spring 2014

This blog post is a place to collect information about the Harvard number theory learning seminar spring 2014. We meet Mondays 4:15-6pm (actual times: if you run on Harvard time, we meet at 4:08) in SC 507.

After a brief intense seminar on Scholze’s thesis and the MSRI conference, we are currently reading the paper of Matt Emerton on Local-Global compatibility for GL_2(Q) in the p-adic Langlands correspondence.

While nominally being organised by myself, this is now really being run by Erick Knight, to whom all angry complaints and difficult questions about the mathematical content and organisation should be addressed. I am still prepared to accept compliments, lavish gifts, etc. and still exercise the right to write dates in the format DD/MM.

 

Schedule of Talks

(2 introductory talks by Erick on the general p-adic Langlands program)

24/03 – Introduction, Completed cohomology and promodular representations (Rong)

31/03 – ”p-adic Langlands done badly” for GL_2(Ql) (Cheng-Chiang)

07/04 – p-adic Langlands done correctly (Yihang)

14/04 – Completed Hecke Algebras 1 (Koji)

21/04 – Completed Hecke Algebras 2 (Bao?)

28/04 – Proof of Main Theorem (Yunqing)

04/05 – Application to the Fontaine-Mazur Conjecture (Tom)

A new construction of the Witt vectors

In a short article appearing on the arxiv today Cuntz and Deninger seem to give a new simple construction of the ring of Witt vectors. Seems like good news for people like me who use them on a daily basis but would probably need to go looking for a copy of Serre’s “Local Fields” if asked for the details on how to actually construct them. This post represents my processing the definition appearing in their paper.

Firstly, recall that for any perfect -algebra , a strict -ring for is a ring in which is not a zero-divisor, Hausdorff and complete for the -adic topology, and with . The key fact about these rings is the following.

Proposition: For every perfect -algebra , a strict -ring exists, and is unique up to unique isomorphism as a ring over (in fact is a functor).

This is of course well-known. The new construction goes as follows. View as a monoid (remember multiplication and the identity element), and form the free ring thereon. This has elements with addition as a “free -module” and multiplication coming from the monoid structure. For example, this means that weirdly yet (but ). There is also (induced from the identity on as a monoid) a natural ring map . Let be its kernel, and form the -adic completion . It turns out (and the proof in their paper is pretty short) that this is a strict -ring and so canonically isomorphic to .

One interesting feature of this construction is that of course you can run it for not perfect, where the Witt construction also gives you something but which is non-canonical (a `Cohen ring’). Apparently this construction in general gives a different one from the Witt construction (so it is genuinely different: not a clever repackaging).

Modular forms and p-adic L-functions

In this post I want to advertise Serre’s lovely note, following the opening section which gives a simple definition of p-adic modular forms (via q-expansions) and uses this and some elementary congruences to construct the classical p-adic L-functions. Serre’s writing is excellent so I give only a brief account and let the interested reader consult the master.

The definition goes as follows. Fix a level (in fact, let’s just take level 1), and a prime (which we will take to be odd, but the case appears no harder). By taking q-expansions, one can consider the algebra of classical modular forms of level 1 (all weights and indeed mixed weights) as a subalgebra In fact, flat base change and the construction of models for modular curves implies one can actually do this on the integral and rational levels in such a way as loses no information: one is naturally led to study and . But now note that , a subring of which can be equipped with the structure of a Banach algebra via the ‘sup norm’ (the distance between and is the largest value of ).

It thus makes sense to consider the closure of with respect to this topology, and it is this which Serre defines to be the algebra of -adic modular forms. In other words, a p-adic modular form is just a power series with p-adic coefficients which can be approximated uniformly coefficient-wise by the q-expansions of classical modular forms.

Pure classical modular forms have a weight . What about p-adic modular forms? One crucial computation in Serre’s paper that makes the theory work says that if two modular forms are congruent modulo a large power of then their weights are also congruent modulo a large power of and also modulo . From this one can easily attach a weight in the group to a p-adic modular form (and since we are working at level 1, all weights arising will be even (so the subgroup on the first factor is all that is hit). We should remark that this computation has as an input the classical theorem of Clausen-von Stadt on the denominators of Bernoulli numbers.

Another interesting consequence of this which Serre notes is the following. Suppose we have a power series and we would like to show it’s a p-adic modular form. Maybe we can write it as a putative limit of some modular forms , except we only know that for all the coefficients converge (but know nothing about the constant coefficients). Suppose further we also know the weights converge to some nonzero .

Well then the weight zero modular form and cannot be too close p-adically, where the length scale implicit in the phrase ‘too close’ is given with reference to one of the modular forms in question, so one gets a bound of the form , where is some constant depending on how far is from zero. Applying this to our sequence we learn in particular that the $a^i_0$ lie in a closed bounded subset of , so there is a convergent subsequence, and passing to the corresponding subsequence of modular forms we deduce that is a p-adic modular form after all.

One could complain that this is a silly theorem: when will we have that all but the constant coefficient is known to converge? Recall the classical weight Eisenstein series, whose q-expansions are given in terms of the Bernoulli numbers and the “sum of th powers of all divisors of ” function :

.

If we take a p-adically convergent sequence of weights that also tends to infinity in the archimedean metric, then one sees explicitly that p-adically:

.

Therefore the sequence of Eisenstein series fit exactly in the situation of the above theorem, and we deduce that there is a p-adic Eisenstein series of any weight , which is well-defined because depends only on . In particular, we deduce the existence of a well-defined continuous p-adic function such that for all . One can check that this is exactly the p-adic zeta function constructed classically by Kubota-Leopoldt and featuring on the analytic side of the main conjecture of Iwasawa theory.